A JavaScript program that checks whether a given number is a prime number or not, which is helpful in various applications such as cryptography, computer security, and data encryption.
Here are four different JavaScript programs that check if a given number is a prime number or not:
1. Using JavaScript for loop
In this example, we define a function isPrime that takes a number as an argument and returns true if the number is prime, and false otherwise.
We start by checking if the number is less than or equal to 1, as these values are not considered prime. If the number is greater than 1, we use a for loop to check if it is divisible by any number other than 1 and itself. If it is, the function returns false. If the loop completes without finding any divisors, the function returns true.
function isPrime(num) {
if (num <= 1) {
return false;
}
for (let i = 2; i < num; i++) {
if (num % i === 0) {
return false;
}
}
return true;
}
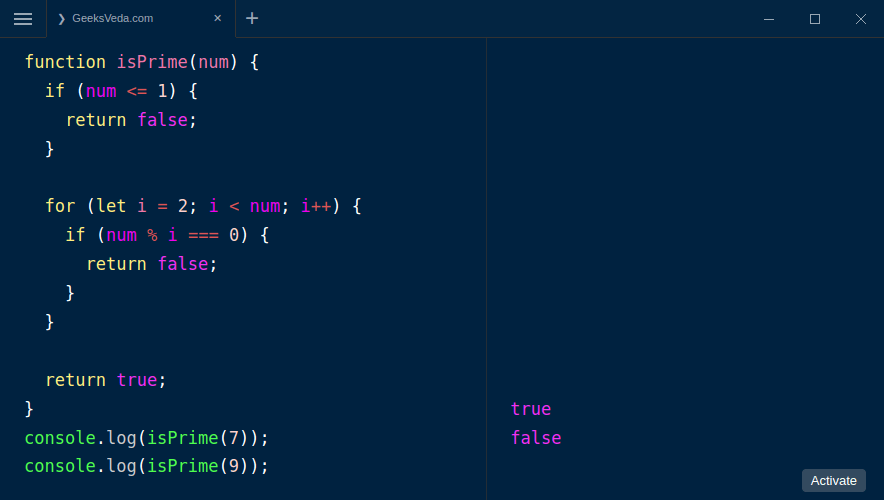
console.log(isPrime(7));
console.log(isPrime(9));
For example, you can call the above code in the console with any number as the argument. We will use 7 and 9 for this example as shown in the illustration.
2. Using JavaScript while loop
The second method is similar to the previous one but uses a while loop instead of a for loop to check divisibility. We start by checking if the number is less than or equal to 1, as these values are not considered prime.
We then initialize a variable divisor to 2 and used a while loop to check if the number is divisible by any number other than 1 and itself. If it is, the function returns false. If the loop completes without finding any divisors, the function returns true.
function isPrime(num) {
if (num <= 1) {
return false;
}
let divisor = 2;
while (divisor < num) {
if (num % divisor === 0) {
return false;
}
divisor++;
}
return true;
}
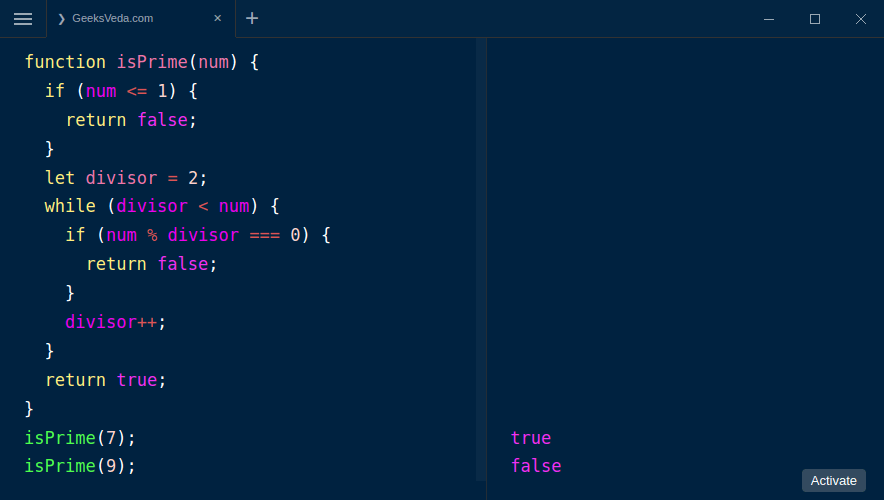
isPrime(7);
isPrime(9);
Below is an example of how this method is executed in the console.
3. Using JavaScript Brute Force Method
This method involves checking all possible divisors of the number up to its square root. If any divisor other than 1 and the number itself is found, the number is not a prime.
function isPrime(num) {
if (num <= 1) {
return false;
}
for (let i = 2; i <= Math.sqrt(num); i++) {
if (num % i === 0) {
return false;
}
}
return true;
}
isPrime(7);
isPrime(9);
In this example, we define a function isPrime that takes a number as an argument and returns true if the number is a prime and false otherwise.
We first check whether the number is less than or equal to 1, in which case it is not a prime. We then loop from 2 to the square root of the number and check whether the number is divisible by any of the integers in that range. If a divisor is found, the number is not a prime, and we return false. If no divisor is found, the number is a prime, and we return true.
4. Using JavaScript Sieve of Eratosthenes
This method involves generating a list of prime numbers up to a given limit and checking whether the number is in the list.
function sieveOfEratosthenes(limit) {
let primes = [];
let isPrime = new Array(limit + 1).fill(true);
isPrime[0] = false;
isPrime[1] = false;
for (let i = 2; i <= limit; i++) {
if (isPrime[i]) {
primes.push(i);
for (let j = i * i; j <= limit; j += i) {
isPrime[j] = false;
}
}
}
return primes;
}
function isPrime(num) {
let primes = sieveOfEratosthenes(num);
return primes.includes(num);
}
isPrime(7);
sieveOfEratosthenes(20);
In this example, we define two functions. The first function, sieveOfEratosthenes, generate a list of prime numbers up to a given limit using the Sieve of Eratosthenes algorithm.
The algorithm involves initializing an array of Boolean values indicating whether each number up to the limit is a prime and then iterating over the array to mark multiples of each prime number as non-prime. The prime numbers are then collected in an array and returned.
The second function, isPrime, takes a number as an argument, generates a list of primes up to the number using the sieveOfEratosthenes function, and checks whether the number is in the list using the includes method.
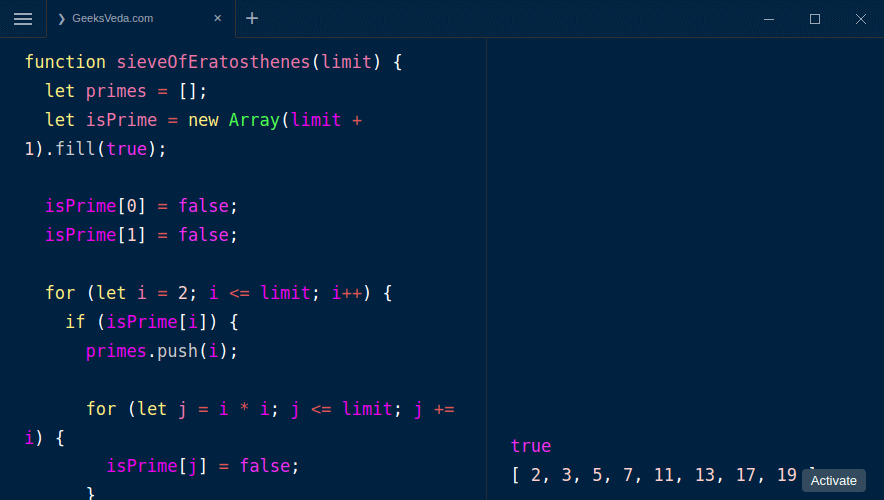
If you call isPrime alone in the console, the system will return a true or false output to indicate whether the number is prime or not.
On the other hand, if you call sieveOfErastothenes with a specific number as the argument then you will obtain a list of all the prime numbers preceding the number.
Conclusion
Finding whether a number is prime or not is a common problem in mathematics and computer science. However, with the help of JavaScript, we can easily create a program that checks whether a given number is prime.
By implementing various techniques such as the trial division method and Sieve of Eratosthenes, we can efficiently check for prime numbers in JavaScript. Overall, having the ability to identify prime numbers is a useful skill for anyone interested in mathematics or programming.
Do you have any other methods to check if a number is a prime number? you would want us to include in this article? Please share it in the comment box below.
