The Fibonacci sequence is a mathematical concept that provides a playground for programmers who want to observe its pattern and explore its practical examples.
Today’s guide is all about printing the Fibonacci sequence in Python. From the Recursion method, Iteration, Memoization, and the efficiency of Dynamic Programming, we will demonstrate all of the specified methods with examples.
So, let’s dive deep into algorithmic thinking, and the relationship between code and numbers.
What is the Purpose of the Fibonacci Sequence in Python
Before moving towards the approaches utilized for printing the Fibonacci sequence in Python, we will list out its use cases as follows:
- Foundational Learning – Introduction to recursion and iteration for newcomers.
- Algorithmic Insight – Understanding of algorithms through recursive and iterative methods.
- Pattern Unveiling – Recognition of patterns within data through the sequence.
- Mathematical Wonder – Appreciation for mathematical beauty and relevance.
- Coding Challenges – Confidence to tackle Fibonacci-based coding problems.
- Diverse Applications – Toolkit expansion for data analysis, cryptography, and more.
- Dynamic Optimization – Proficiency in optimizing solutions with dynamic programming.
- Visualized Education – Vivid math illustration for educators.
- Advanced Exploration – Gateway to intricate mathematical topics.
- Practical Skill Transfer – Enhanced coding skills for various projects.
How to Print the Fibonacci Sequence in Python
In order to display the Fibonacci sequence in Python, you can use:
- Iteration
- Memoization
- Dynamic Programming
- Recursion
Let’s check out each method with practical examples!
1. Using Recursion Method
Recursion is considered a simple approach for displaying or showing the Fibonacci sequence. A recursive function calculates each term based on the sum of the recent or last two terms.
More specifically, by breaking down the problem into smaller subproblems, this method holds the sequence’s inherent recursive structure.
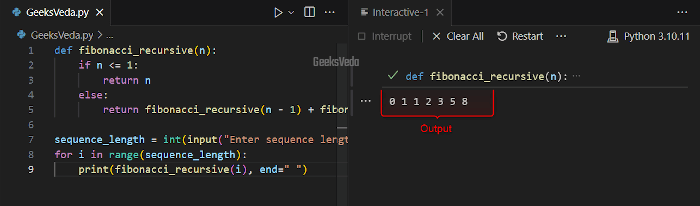
For instance, in the following example, we have a “fibonacci_recursive()” function that will calculate the Fibonacci sequence using recursion. The base case of this function makes sure that the correct values for the first two terms “0” and “1” will be returned.
On the other hand, the subsequent terms will be obtained by recursively summing up the last two terms.
def fibonacci_recursive(n):
if n <= 1:
return n
else:
return fibonacci_recursive(n - 1) + fibonacci_recursive(n - 2)
sequence_length = int(input("Enter sequence length: "))
for i in range(sequence_length):
print(fibonacci_recursive(i), end=" ")
Here, we will enter “7” as the Fibonacci sequence length. As a result, the Fibonacci sequence will be displayed on the console.
2. Using Iteration Method
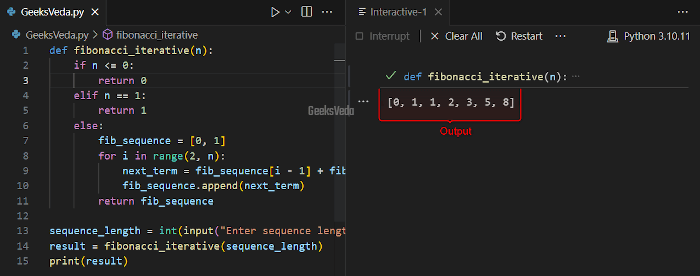
Iterative methods offer a practical way of printing the Fibonacci sequence. By starting with the initial terms and then moving toward the subsequent terms, this method avoids the overhead of the function calls.
Here the “fibonacci_iterative()” function calculates the Fibonacci sequence iteratively. It initializes a list with the first two terms and then generates the subsequent terms by adding the last two.
def fibonacci_iterative(n):
if n <= 0:
return 0
elif n == 1:
return 1
else:
fib_sequence = [0, 1]
for i in range(2, n):
next_term = fib_sequence[i - 1] + fib_sequence[i - 2]
fib_sequence.append(next_term)
return fib_sequence
sequence_length = int(input("Enter sequence length: "))
result = fibonacci_iterative(sequence_length)
print(result)
3. Using Memoization Method
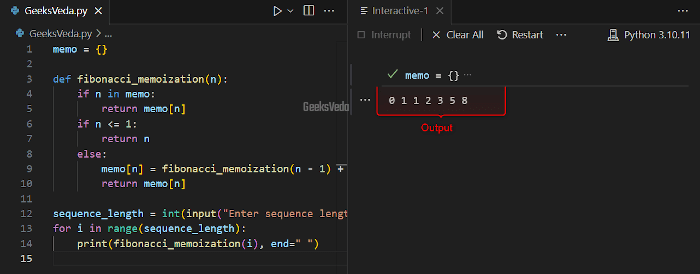
Memoization is an optimized approach that stores the previously computed values to avoid redundant calculations. For example, in the provided code, the “fibonacc_memoization()” function utilized a dictionary named “memo” for storing the calculated values.
While calculating the terms, the function checks if the value is already in “memo” before performing the calculator.
memo = {}
def fibonacci_memoization(n):
if n in memo:
return memo[n]
if n <= 1:
return n
else:
memo[n] = fibonacci_memoization(n - 1) + fibonacci_memoization(n - 2)
return memo[n]
sequence_length = int(input("Enter sequence length: "))
for i in range(sequence_length):
print(fibonacci_memoization(i), end=" ")
4. Using Dynamic Programming
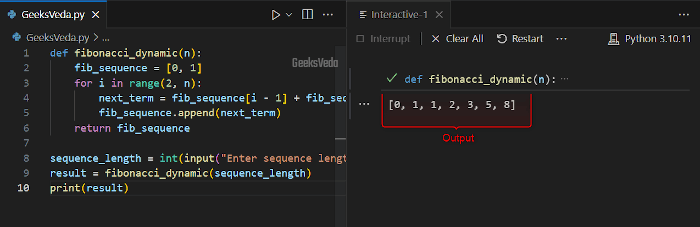
Dynamic programming uses an array for storing the calculated values and ultimately optimizes the Fibonacci calculation.
According to the given code, the “fibonacci_dynamic()” utilizes an array for storing the previously calculated terms. This function iteratively generates the sequence by summing the last two terms and appending the result.
def fibonacci_dynamic(n):
fib_sequence = [0, 1]
for i in range(2, n):
next_term = fib_sequence[i - 1] + fib_sequence[i - 2]
fib_sequence.append(next_term)
return fib_sequence
sequence_length = int(input("Enter sequence length: "))
result = fibonacci_dynamic(sequence_length)
print(result)
Choosing the Right Method to Print the Fibonacci Sequence
Check out the following comparison table for selecting the right method for printing the Fibonacci sequence:
| Method | Advantages | Disadvantages | Use Cases |
| Recursion | Elegance, mirrors sequence definition. | Redundant calculations for larger terms. | Learning recursion, small sequence outputs. |
| Iteration | Efficient, and suitable for larger sequences. | Potential memory overhead for long sequences. | Printing long sequences, avoiding recursion. |
| Memoization | Reduced redundant calculations. | Memory consumption, a more complex approach. | Recursive approach optimization |
| Dynamic Programming | Efficient, eliminate redundant calculations. | Array storage may require larger memory. | Printing large sequences efficiently. |
That brought us to the end of today’s guide related to printing the Fibonacci sequence in Python.
Conclusion
Printing the Fibonacci sequence in Python is a skill that combines the concepts of mathematics and programming. From the Recursion method, Iteration, Memoization, and the efficiency of Dynamic Programming, we have explored all of the mentioned approaches with practical examples.
So, choose the most suitable method and optimize the added algorithms in your Python project.
Want to explore and learn more related to Python, do check out our dedicated Python Tutorial Series!
