In Mathematics and Computer Science, Recursion is a fundamental concept that introduces a robust approach to solving problems. It enables you to break down complex challenges into smaller, more manageable chunks, and create a way for efficient algorithms.
Today, we will explore recursion, its basic principles, applications in data structures, and advanced techniques, specifically in Python.
So, let’s start this learning journey!
What is Recursion in Python
Python Recursion is like a puzzle-solving loop where a function invokes or calls itself to solve complex problems. This concept is similar to Russian nesting dolls, where each doll contains a smaller side.
In Python programming, recursion breaks down problems into simpler versions of themselves, which makes them ideal for handling complicated tasks or operations step by step.
Basic Concepts of Recursion in Python
Let’s discuss some basic concepts related to recursion such as function calls, base and recursive cases, and the call stack.
1. Recursive Functions and Calls
Recursive functions work like magic mirrors that reflect a smaller version of the same puzzle. More specifically, when a function invokes itself, it triggers a series of problem-solving steps.
In such a scenario, each function call operates on its own piece of data that contributes to the bigger solution.
2. Base Cases and Recursive Cases
The concept of base cases is crucial in a successful recursion. Base cases are the simplest forms of the problem that can be directly resolved. However, recursive cases dive into the complexity, break down the problem into smaller chunks, and utilize the same function to solve them.
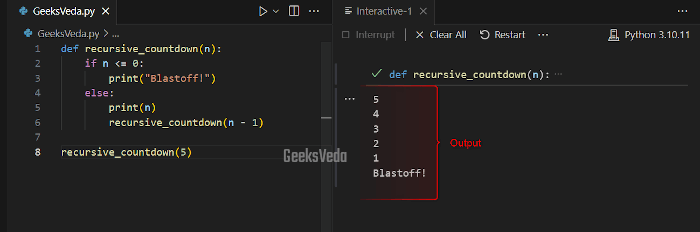
For instance, we will now create a simple countdown using recursive. Here, the “recursive_countdown()” function prints the countdown number and then invokes itself with a smaller number.
In the given program, the base case is when “n” is less than or equal to “0“, which indicates the countdown is complete.
def recursive_countdown(n):
if n <= 0:
print("Blastoff!")
else:
print(n)
recursive_countdown(n - 1)
recursive_countdown(5)
3. The Call Stack in Recursion
Imagine a call stack as the stack of plates, in which each function call is like placing a new plate on top, and when a function returns something, the top plate is removed.
In recursion, each new function call is stacked on the previous one, which creates a chain of problem-solving steps. As function outputs or returns, they are popped off the stack.
Explore the Factorial Function in Python
Factorials might sound like a complex concept, however, with recursion, they become a fascinating puzzle to solve. It is like breaking down a big task into smaller, manageable steps.
So, whether you are calculating the factorial of a small number or a large one, recursion simplifies the process and demonstrates the problem-solving functionality layer by layer.
Recursive Approach for Factorial Calculation
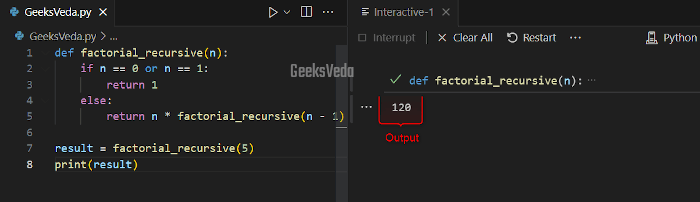
According to the given code, we have a “factorial_recursive()” function that calculates the factorial of a number with recursion. This function starts by checking if “n” is 0 or 1 and returns 1 in these cases.
However, for the values of “n“, the function multiples “n” by the factorial of “n – 1” which ultimately creates a chain of calculations.
def factorial_recursive(n):
if n == 0 or n == 1:
return 1
else:
return n * factorial_recursive(n - 1)
result = factorial_recursive(5)
print(result)
This recursive process continues until the base case is reached.
The Fibonacci Sequence
The Fibonacci sequence is represented by a series of numbers that appears in nature’s pattern and mathematics alike. More specifically, with recursion, you can generate these numbers and explore different optimization techniques that make the calculation of Fibonacci values more optimized.
1. Solve Fibonacci with Recursion
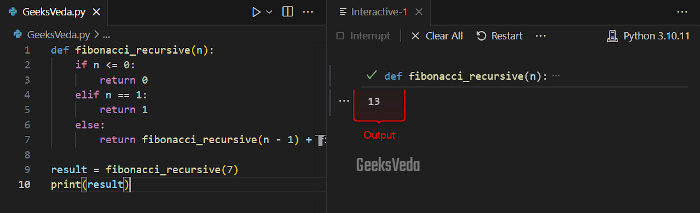
In the given code, the “fibnonacci_recursive()” function calculates the Fibonacci sequence with the help of recursion. Base case has been defined for when “n” is 0 or 1.
For other values, the function will invoke itself with smaller values and add the results of two previous numbers.
def fibonacci_recursive(n):
if n <= 0:
return 0
elif n == 1:
return 1
else:
return fibonacci_recursive(n - 1) + fibonacci_recursive(n - 2)
result = fibonacci_recursive(7)
print(result)
This recursive process continues until the desired Fibonacci number is reached.
2. Memoization: Optimizing Recursive Fibonacci
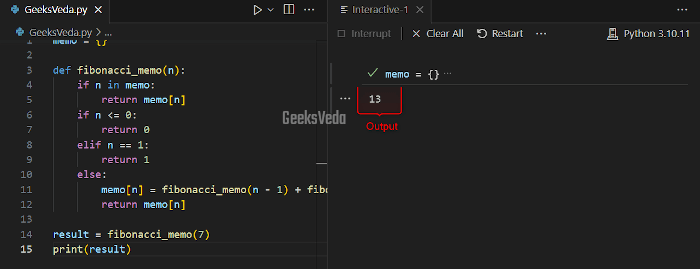
Memoization improves the recursive Fibonacci by storing previously calculated values in a dictionary named “memo“. Before making a recursive call, the function verifies if the result is already in the memo.
Resultantly, this optimization minimizes the redundant calculator and speeds up the calculation process.
memo = {}
def fibonacci_memo(n):
if n in memo:
return memo[n]
if n <= 0:
return 0
elif n == 1:
return 1
else:
memo[n] = fibonacci_memo(n - 1) + fibonacci_memo(n - 2)
return memo[n]
result = fibonacci_memo(7)
print(result)
When to Choose Recursion or Iteration
Check out the table to learn about the use cases of recursion and iteration:
| Situation | Recursion | Iteration |
| Solving complex problems. | Well-suited for problems that can be divided into smaller, similar subproblems. | Effective for linear, step-by-step tasks. |
| Tree-like data structures | Ideal for traversing and manipulating hierarchical structures. | Suitable for looping through collections. |
| Mathematical calculations | Great for problems with recursive mathematical formulas. | Suitable for straightforward calculations. |
| Divide and conquer algorithms | Effective for algorithms that divide problems into smaller instances. | Useful for controlled, sequential tasks. |
| Clear problem representation | Well-suited when the problem can be naturally described in a recursive manner. | Preferable when problems have clear loops. |
Handling Complex Problems with Python Recursion
As mentioned earlier, recursion can be utilized for handling complex problems. Now, in this section, we will check out how recursion can be used in divide and conquer, dealing with tree structures, and implementing advanced algorithms like merge sort and binary search.
Divide and Conquer Strategy
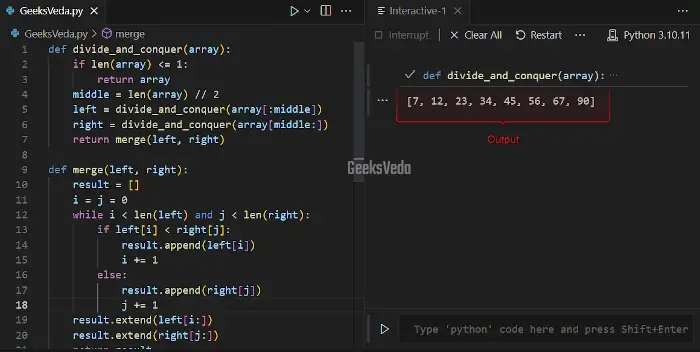
In the following program, the “divide_and_conquer()” function demonstrates the divide and conquer strategy with recursion. It divides the array into small halves or portions until it reaches single elements.
Then, the “merge()” function combines these smaller sorted arrays back together.
def divide_and_conquer(array):
if len(array) <= 1:
return array
middle = len(array) // 2
left = divide_and_conquer(array[:middle])
right = divide_and_conquer(array[middle:])
return merge(left, right)
def merge(left, right):
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result.extend(left[i:])
result.extend(right[j:])
return result
array = [12, 45, 23, 7, 56, 34, 67, 90]
sorted_array = divide_and_conquer(array)
print(sorted_array)
2. Binary Search
The “binary_search()” function applies binary search using recursion. It looks for a target value in a sorted array by repeatedly dividing the search range in half and narrowing down the search until the target is found or the search range turns empty.
def binary_search(array, target, low, high):
if low > high:
return -1
mid = (low + high) // 2
if array[mid] == target:
return mid
elif array[mid] < target:
return binary_search(array, target, mid + 1, high)
else:
return binary_search(array, target, low, mid - 1)
array = [2, 5, 8, 12, 16, 23, 38, 56, 72, 91]
target = 23
index = binary_search(array, target, 0, len(array) - 1)
if index != -1:
print(f"Element {target} found at index {index}")
else:
print(f"Element {target} not found in the array")
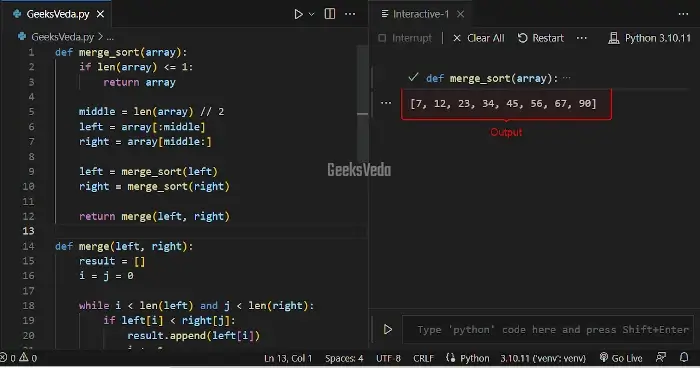
3. Merge Sort
In this example, the “merge_sort()” function performs merge sort with recursion. It divides the created array into two halves, recursively sorts them, and then merges them back together with the help of the “merge()” function.
def merge_sort(array):
if len(array) <= 1:
return array
middle = len(array) // 2
left = array[:middle]
right = array[middle:]
left = merge_sort(left)
right = merge_sort(right)
return merge(left, right)
def merge(left, right):
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result.extend(left[i:])
result.extend(right[j:])
return result
array = [12, 45, 23, 7, 56, 34, 67, 90]
sorted_array = merge_sort(array)
print(sorted_array)
4. Recursive Tree Structures
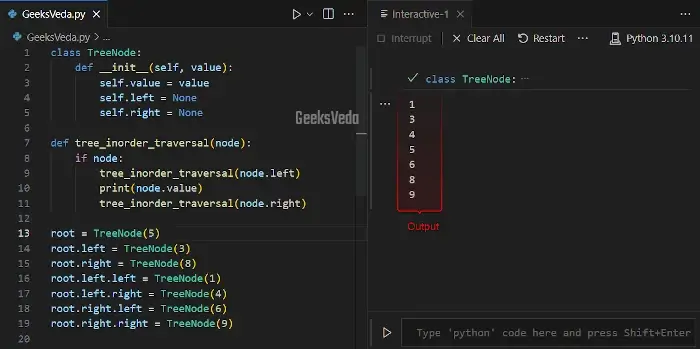
Recursion can be also applied to tree-like structures, such as binary trees. Additionally, traversing, searching, and manipulating such structures can be done with recursive techniques.
The following example demonstrates an in-order traversal of a binary tree with recursion. The “tree_inorder_traversal()” function visits each node in the left sub-tree, then the relevant current node, and lastly the nodes in the right subtree.
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def tree_inorder_traversal(node):
if node:
tree_inorder_traversal(node.left)
print(node.value)
tree_inorder_traversal(node.right)
root = TreeNode(5)
root.left = TreeNode(3)
root.right = TreeNode(8)
root.left.left = TreeNode(1)
root.left.right = TreeNode(4)
root.right.left = TreeNode(6)
root.right.right = TreeNode(9)
tree_inorder_traversal(root)
Python Recursion in Data Structures
Python also permits you to understand and manipulate data structures using recursion. From linked lists to trees, recursion enables the programmers to traverse, search, and manipulate these structures.
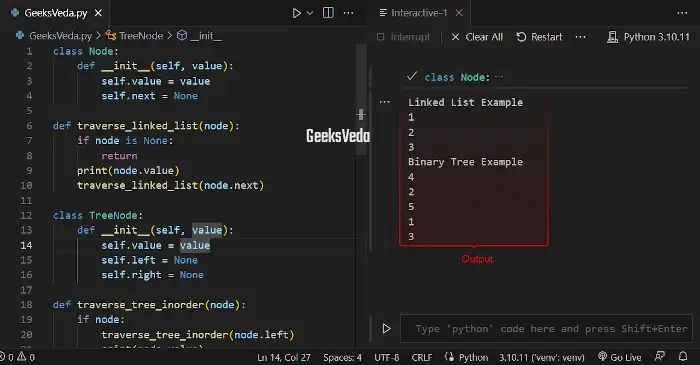
1. Recursion in Linked Lists and Trees
According to the given program, the “traverse_linked_list()” function traverses a linked list utilizing recursion. Note that each node will be printed and the function involves itself with the next node.
For the tree, the “traverse_tree_inorder()” function performs an inorder traversal and displays the values of the nodes in ascending order.
class Node:
def __init__(self, value):
self.value = value
self.next = None
def traverse_linked_list(node):
if node is None:
return
print(node.value)
traverse_linked_list(node.next)
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def traverse_tree_inorder(node):
if node:
traverse_tree_inorder(node.left)
print(node.value)
traverse_tree_inorder(node.right)
print('Linked List Example')
head = Node(1)
head.next = Node(2)
head.next.next = Node(3)
traverse_linked_list(head)
print('Binary Tree Example')
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
traverse_tree_inorder(root)
2. Traversal and Search Recursive Structures
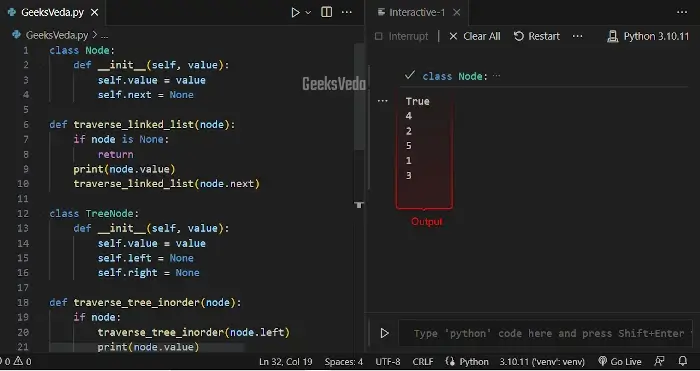
Here, the “search_tree()” function recursively searches for a target value in a binary tree. It outputs “True” if the target has been found in the tree and “False” in the other case.
class Node:
def __init__(self, value):
self.value = value
self.next = None
def traverse_linked_list(node):
if node is None:
return
print(node.value)
traverse_linked_list(node.next)
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def traverse_tree_inorder(node):
if node:
traverse_tree_inorder(node.left)
print(node.value)
traverse_tree_inorder(node.right)
def search_tree(node, target):
if node is None:
return False
if node.value == target:
return True
return search_tree(node.left, target) or search_tree(node.right, target)
# Binary Tree Search Example
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
result = search_tree(root, 3)
print(result)
root.left.right = TreeNode(5)
traverse_tree_inorder(root)
3. Recursive Algorithms for Data Manipulation
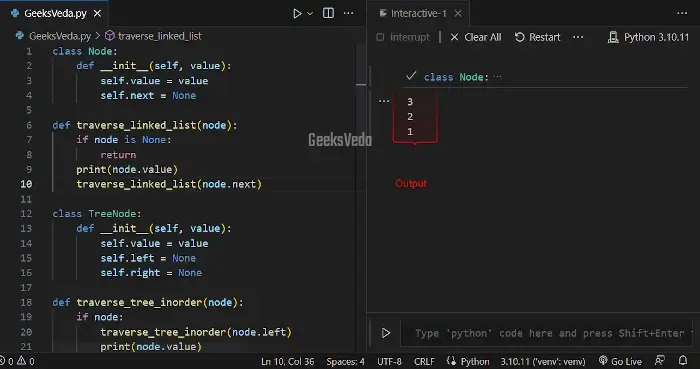
In the provided code, the “reverse_linked_list()” reverse the given linked list using recursion. It outputs the new head of the reversed list by reversing the links between nodes.
class Node:
def __init__(self, value):
self.value = value
self.next = None
def traverse_linked_list(node):
if node is None:
return
print(node.value)
traverse_linked_list(node.next)
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def traverse_tree_inorder(node):
if node:
traverse_tree_inorder(node.left)
print(node.value)
traverse_tree_inorder(node.right)
def search_tree(node, target):
if node is None:
return False
if node.value == target:
return True
return search_tree(node.left, target) or search_tree(node.right, target)
def reverse_linked_list(node):
if node is None or node.next is None:
return node
rest = reverse_linked_list(node.next)
node.next.next = node
node.next = None
return rest
# Reversing Linked List Example
head = Node(1)
head.next = Node(2)
head.next.next = Node(3)
new_head = reverse_linked_list(head)
traverse_linked_list(new_head)
That brought us to the end of our today’s guide related to Python recursion.
Conclusion
In Python, recursion is a technique that can be utilized for problem-solving. As a programmer, it is essential for you to understand the basics of recursion to use it within the various data structures.
With the help of our guide, you can explore, experiment, and apply recursion principles to conquer the most complicated tasks.
Want to explore and learn more related to Python, do check out our dedicated Python Tutorial Series!
