In different real-world fields, such as Physics, Geometry, and Computer Graphics, calculating the area of a triangle is considered a fundamental concept.
More specifically, if you are building your project in Python, you can use its powerful libraries to compute the area of a triangle.
Today’s guide is all about calculating the area of a triangle using different techniques in Python. Start this learning journey and gain a comprehensive understanding of the relevant approaches!
Why Calculate Triangle Area in Python
Whether you are designing structures, creating visualizations, or plotting graphs, knowing how to calculate triangle area is a valuable skill in Python.
For instance, calculating triangle area is essential for understanding shapes and spatial relationships. Area computation finds applications in fields like geometry, physics, and computer graphics as it helps in construction, land measurement, and design.
Last but not least, learning area calculation improves mathematical problem-solving skills.
How to Calculate Triangle Area in Python
Python offers multiple approaches for calculating triangle area in Python. For instance, you can utilize:
- Base and Height
- Heron’s formula
- Coordinates of vertices
- Trigonometric approaches
Let’s explore each of the mentioned methods individually!
1. Using Base and Height
In Python, one of the simplest methods for calculating triangle area is using its base and respective height. More specifically, the formula “area = 0.5 * base * height” permits you to compute the area effectively.
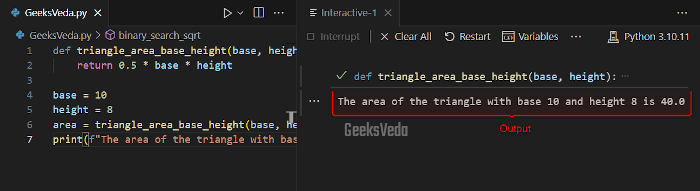
For instance, we will define a function named “triangle_area_base_height()” that calculates the area of the triangle with the help of the defined base and height.
This function then implements the mentioned formula and outputs the resultant value.
def triangle_area_base_height(base, height):
return 0.5 * base * height
base = 10
height = 8
area = triangle_area_base_height(base, height)
print(f"The area of the triangle with base {base} and height {height} is {area}")
It can be observed that we have passed base and height values as “10” and “8” and the area of the triangle has been displayed as “40.0“.
2. Using Heron’s Formula
Heron’s formula is another robust technique for calculating the area of the triangle using its side length. This approach works by considering the semi-perimeter and applying some mathematical formula on the side lengths.
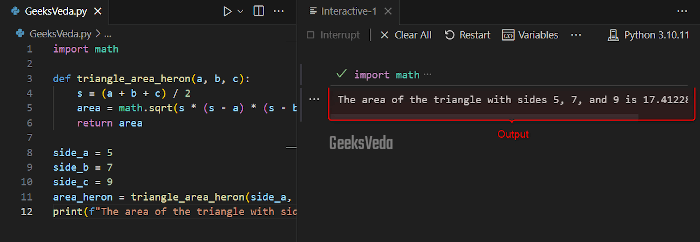
Here, we have a “triangle_area_heron()” function that implements Heron’s formula for calculating the area of the triangle with respect to its side lengths.
This formula specifically utilizes the “semi-perimeters” and the side length as “a“, “b“, and “c” for finding area.
The “math” module has been imported for invoking the “sqrt()” method for taking the square of the value. Lastly, the print() function displays the returned value of the triangle area on the console.
import math
def triangle_area_heron(a, b, c):
s = (a + b + c) / 2
area = math.sqrt(s * (s - a) * (s - b) * (s - c))
return area
side_a = 5
side_b = 7
side_c = 9
area_heron = triangle_area_heron(side_a, side_b, side_c)
print(f"The area of the triangle with sides {side_a}, {side_b}, and {side_c} is {area_heron}")
3. Using Coordinates of Vertices
The approach of calculating the triangle area using coordinates or vertices is based on the “Shoelace” formula. This approach transforms the coordinate geometry into the triangle area calculation.
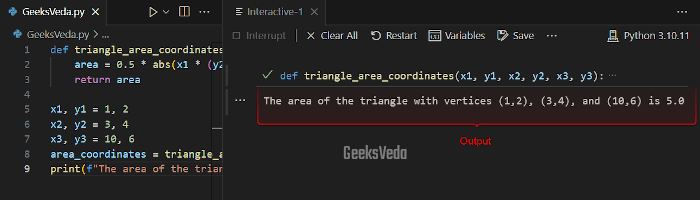
According to the given code, we have a function named “triangle_area_coordinates()” that calculates the triangle area according to the Shoelace formula. This formula evaluates the sum of products based on coordinates that yield the area.
This function is invoked by passing the coordinates of vertices as arguments. Resultantly, the returned area values will be shown on the console with the “print()” function.
def triangle_area_coordinates(x1, y1, x2, y2, x3, y3):
area = 0.5 * abs(x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2))
return area
x1, y1 = 1, 2
x2, y2 = 3, 4
x3, y3 = 10, 6
area_coordinates = triangle_area_coordinates(x1, y1, x2, y2, x3, y3)
print(f"The area of the triangle with vertices ({x1},{y1}), ({x2},{y2}), and ({x3},{y3}) is {area_coordinates}")
4. Using Trigonometric Approaches
Another technique for finding the area of a triangle is based on trigonometry and the sine function. By following this approach, it is possible to calculate the area of a triangle using side lengths and angles.
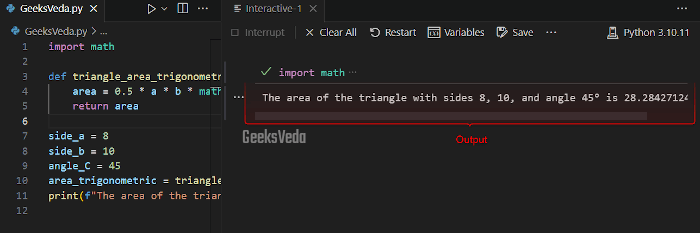
For instance, here, we have a function named “triangle_area_trigonometric()” that calculates the triangle area with respect to the specified side lengths “a” and “b” and the included “angle“.
This formula uses the “math.sin()” function and the accepted arguments and returns the area value.
import math
def triangle_area_trigonometric(a, b, angle):
area = 0.5 * a * b * math.sin(math.radians(angle))
return area
side_a = 8
side_b = 10
angle_C = 45
area_trigonometric = triangle_area_trigonometric(side_a, side_b, angle_C)
print(f"The area of the triangle with sides {side_a}, {side_b}, and angle {angle_C}° is {area_trigonometric}")
Choose the Right Method to Calculate the Triangle Area
Have a look at the comparison table of the above-discussed approaches to calculate the triangle area.
| Approach | Method Description | Pros | Cons |
| Using Base and Height | Utilizes the base and height of the triangle. | Simple and intuitive. | Requires direct measurements. |
| Heron’s Formula | Utilizes side lengths and semi-perimeter. | Works for any type of triangle. | Involves square root calculation. |
| Coordinates of Vertices | Uses vertex coordinates and shoelace formula. | Works for arbitrary triangles. | Requires knowledge of coordinate geometry. |
| Trigonometric Approaches | Involves sin() function and side lengths/angle. | Useful for angles and sides. | Requires knowledge of trigonometry. |
This brought us to the end of our today’s guide related to calculating the area of a triangle in Python.
Conclusion
In Python, you can utilize different techniques for calculating the area of a triangle. Whether you choose the base and height method because of its simplicity, the elegance of Heron’s formula, the precision of the coordinates approach, or the trigonometric methods, Python supports tools for all these scenarios.
So, select the right approach according to the given data and requirements and calculate the area of a triangle confidently!
Want to explore and learn more related to Python, do check out our dedicated Python Tutorial Series!
