In Python programming, the ability to check prime numbers is considered a fundamental skill. It can be used in different scenarios where it is required to optimize algorithms, secure cryptography, and perform data filtering efficiently.
Today’s guide is about checking prime numbers in Python. From looping and modulo operations to advanced techniques such as the Sieve of Eratosthenes algorithm and primality test functions, we will discuss each method with practical examples.
Why Do We Search for Prime Numbers in Python
Prime numbers are those digits divisible only by themselves and 1. These numbers hold a special place in both programming and mathematics.
More specifically, prime numbers are utilized in different use cases as listed below:
- Cryptography and Security – Prime numbers are central to encryption algorithms, ensuring secure communications and data protection.
- Optimization Algorithms – Prime numbers contribute to solving optimization problems, reducing complexity in various scenarios.
- Random Number Generation – Prime numbers play a role in generating pseudo-random sequences for simulations and games.
- Data Filtering – Prime number checks are used to filter out non-prime numbers from datasets, enhancing data quality.
- Hashing Functions – Prime numbers help create effective hashing functions, facilitating efficient data retrieval.
- Number Theory – Prime numbers have deep connections with number theory, inspiring mathematical research, and exploration.
How to Check Prime Numbers in Python
For the purpose of checking prime numbers in Python, you can use:
- Loop and Modulo Operator
- Square Root and Loop
- Sieve of Eratosthenes Algorithm
- Primality Test Functions
Let’s check out all of them practically!
1. Using Loop and Modulo Operator
One of the most simple approaches for checking prime numbers is to loop through the potential divisors with for loop and apply the modulo operator “%“. More specifically, by dividing the number by integers ranging from 2 to the square of the number and checking for zero remainders, it can be evaluated if the number is prime or not.
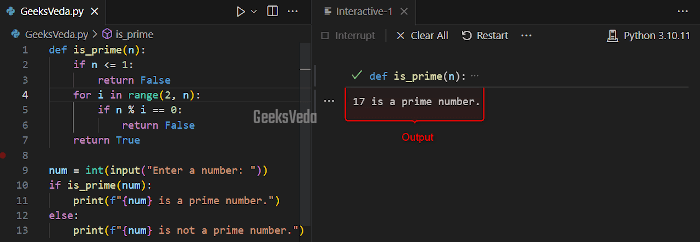
For instance, in the following program, we will define a function named “is_prime()” that uses a for loop and the Modulo operator for verifying if the input number is a prime number.
It iterates from 2 to the square root of the number and checks if any divisor divides without a remainder.
def is_prime(n):
if n <= 1:
return False
for i in range(2, n):
if n % i == 0:
return False
return True
num = int(input("Enter a number: "))
if is_prime(num):
print(f"{num} is a prime number.")
else:
print(f"{num} is not a prime number.")
2. Using Square Root and Loop
This approach can be utilized for optimizing the prime number checks by limiting the range to the square root of the number tested. Additionally, shortening the loop reduces unnecessary calculations and improves overall efficiency.
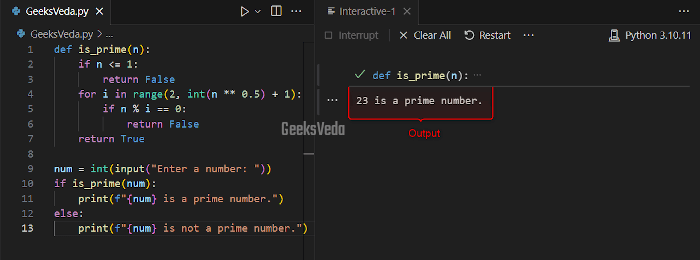
Now, in the same function, we will narrow down the range of the divisors to the square root of the number. This results in more efficient prime number checks.
def is_prime(n):
if n <= 1:
return False
for i in range(2, int(n ** 0.5) + 1):
if n % i == 0:
return False
return True
num = int(input("Enter a number: "))
if is_prime(num):
print(f"{num} is a prime number.")
else:
print(f"{num} is not a prime number.")
3. Using Sieve of Eratosthenes Algorithm
The Sieve of Eratosthenes algorithm employs a unique approach for finding the prime number. For this, it eliminates the non-prime numbers in an efficient manner.
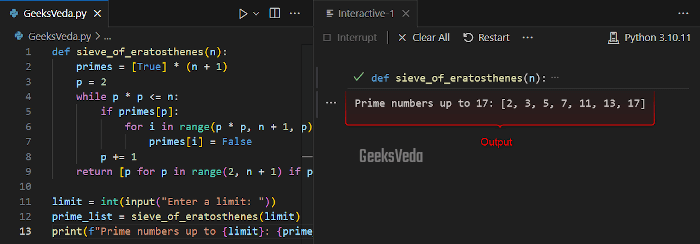
Here, we have used the Sieve of Eratosthenes algorithm to first generate prime numbers up to the given “n” limit. Then, we initiated an array named “primes” for tracking the prime status. Starting with the first prime “p“, as “2“, will be marked as “non-prime“.
After this, the while loop will continue until the square of the prime surpasses “n“. Resultantly, you will see a list of prime numbers within the given limit.
def sieve_of_eratosthenes(n):
primes = [True] * (n + 1)
p = 2
while p * p <= n:
if primes[p]:
for i in range(p * p, n + 1, p):
primes[i] = False
p += 1
return [p for p in range(2, n + 1) if primes[p]]
limit = int(input("Enter a limit: "))
prime_list = sieve_of_eratosthenes(limit)
print(f"Prime numbers up to {limit}: {prime_list}")
After executing the program, we entered “17” which consequently displayed the list of prime numbers till 17.
4. Using Primality Test Functions
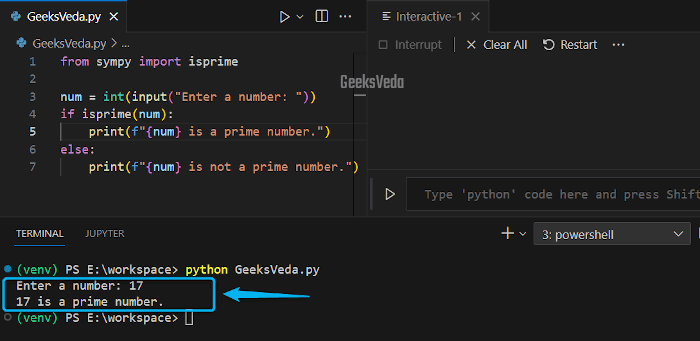
The “Sympy” Python library offers the “isprime()” built-in primality function that can be invoked for validating if the number entered by the user is prime or not.
Here, we will accept input from the users and utilize the if-else condition for the testing.
isprime()” returns “True“, the given number will be considered prime, otherwise, it will be evaluated as a non-prime number.
from sympy import isprime
num = int(input("Enter a number: "))
if isprime(num):
print(f"{num} is a prime number.")
else:
print(f"{num} is not a prime number.")
Choosing the Right Method for Checking Prime Number
Here is a comparison between all of the discussed approaches for selecting the right method for checking prime numbers:
| Method | Advantages | Disadvantages | Use Cases |
| Loop and Modulo Operator |
|
|
Quick checks of primality in small-scale programs or educational contexts. |
| Square Root and Loop |
|
|
Efficient prime checks when dealing with larger numbers and aiming to optimize the loop and computation. |
| Sieve of Eratosthenes Algorithm |
|
|
Generating a list of prime numbers up to a certain limit or optimizing prime number calculations in larger ranges. |
| Primality Test Functions |
|
|
Quick and accurate checks for prime numbers using specialized libraries when high accuracy is essential. |
That brought us to the end of our checking prime numbers in the Python guide.
Conclusion
In this guide, we have explored different techniques for checking prime numbers in Python. From looping and modulo operations to advanced techniques such as the Sieve of Eratosthenes algorithm and primality test functions, all of the mentioned approaches have been demonstrated with practical examples.
Now, utilize any of these as per your project requirement and make informed decisions, optimize solutions, and explore mathematical operations with ease.
Want to explore and learn more related to Python, do check out our dedicated Python Tutorial Series!
