In Mathematics, finding square roots is a fundamental concept that helps you to understand the relationships between numbers. This concept can be implemented for solving complex geometrical or scientific problems.
Python offers several approaches for calculating square roots efficiently. From using built-in functions such as “math.sqrt()“, “numpy.sqrt()“, to the Newton-Raphson method, and the Binary search-based approach, this guide will demonstrate all methods with practical examples.
So, let’s start learning!
What is Square Root in Python
The square root is a basic mathematical operation that holds a significant place in number theory and can be utilized in several practical applications. This concept is applied in fields such as physics, geometry, data analysis, and engineering, wherever it is required to understand the relationship between numbers.
More specifically, in Python, a square root is a number that refers to the process of finding a value that yields the original number when multiplied by itself.
Mathematical Representation of Square Root
The square root of the number “a” can be represented mathematically as “√a“. However, in Python, this mathematical representation is translated by utilizing different techniques that assist in calculating the square roots programmatically.
For this purpose, different algorithms and mathematical functions are used to approximate the square root accurately, even for large or complex numbers
How to Find Square Root in Python
In order to find the square root in Python, you can use:
- Built-in functions
- Newton-Raphson Method
- Babylonian Method
- Binary Search-Based Approach
Let’s look at each of them individually!
1. Using Python Built-in Functions
The standard library of Python offers several built functions which help in simplifying complex operations such as calculating the square root. These functions mainly include “math.sqrt()” and “numpy.sqrt()“.
Using these functions, you can accurately perform the mentioned mathematical operator and also save time and effort.
math.sqrt() Function
Python’s “math” module supports the “sqrt()” function that can be invoked for calculating the square root of a given number. More specifically, by importing this module, you can access the “sqrt()” function and compute the square root.
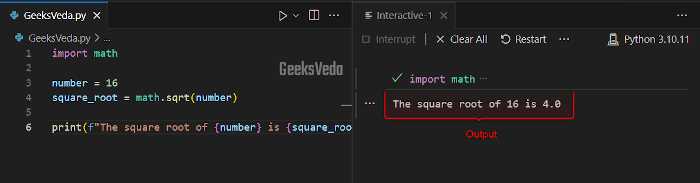
For instance, in the provided code, we first imported the “math” module. After that, the “math.sqrt()” function has been called with the defined “number“, passed as an argument.
import math
number = 16
square_root = math.sqrt(number)
print(f"The square root of {number} is {square_root}")
Consequently, the print() function will display the square root value on the console.
numpy.sqrt() Function
NumPy is a robust Python library that provides different functions for handling arrays and complex mathematical operations. Additionally, its “sqrt()” function can be used for finding the square root of a given number.
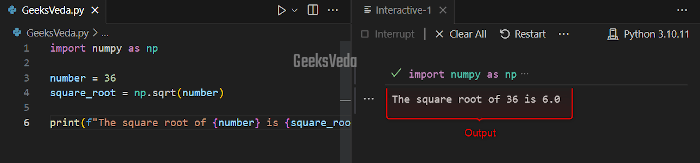
Here, in the given program, firstly, we will import the “numpy” module as “np“. Then, define a number and pass it to the “np.sqrt()” function for calculating its square root.
import numpy as np
number = 36
square_root = np.sqrt(number)
print(f"The square root of {number} is {square_root}")
It can be observed that the square root of 36 has been shown as 6.0.
2. Using Newton-Raphson Method
The Newton-Raphson method is a powerful iterative approach that can be used for approximating square roots. It refines estimates through successive results and quickly processes the results with high accuracy.
According to the given code, we have applied the Newton-Raphson method in the “newton_raphson_sqrt()” function. Within this function:
- “number” refers to the number for which you want to find the square root.
- “guess” with the default value “1” is the initial value for the square root.
- “tol” with the default value “1e-6” is the acceptance or tolerance level of error in the estimate.
Then, the added while loop iterates as long as the absolute difference between the square of the “guess” and the “number” is greater than the defined “tol” value.
Moreover, in each iteration, the value of the “guess” will be updated using the Newton-Raphson formula, which ultimately refines the estimate of the square root.
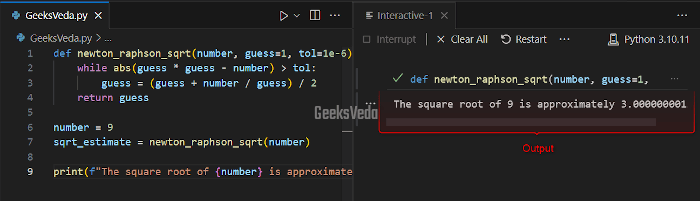
def newton_raphson_sqrt(number, guess=1, tol=1e-6):
while abs(guess * guess - number) > tol:
guess = (guess + number / guess) / 2
return guess
number = 9
sqrt_estimate = newton_raphson_sqrt(number)
print(f"The square root of {number} is approximately {sqrt_estimate}")
After the loop converges to an estimate within the desired tolerance, the function outputs the final “guess” as the estimated square root.
3. Using Babylonian Method
Babylonian is another historical approach that is an older yet effective way of finding square roots in Python. This method is rooted in historical mathematics and is based on the formula of iteratively refining estimates to approach the actual square root.
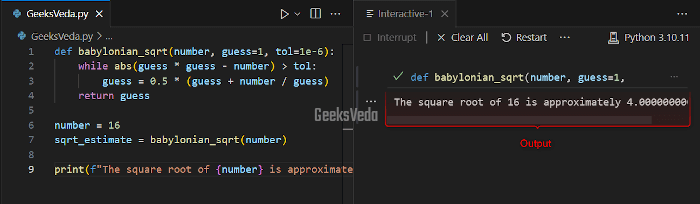
Here, we have defined a function named “babylonian_sqrt()” that estimates the square root of a number with the Babylonian method. This function iteratively refines a guess by calculating the average according to the given formula.
def babylonian_sqrt(number, guess=1, tol=1e-6):
while abs(guess * guess - number) > tol:
guess = 0.5 * (guess + number / guess)
return guess
number = 16
sqrt_estimate = babylonian_sqrt(number)
print(f"The square root of {number} is approximately {sqrt_estimate}")
4. Using a Binary Search-Based Approach
Binary search is a well-known algorithm that can be customized for calculating square roots. For instance, in the provided code, we have defined a “binary_search_sqrt()” function that estimates the square root of the given number.
It repeatedly adjusts the value of the guess by finding the search range in half according to the evaluation of whether the square of the guess is too high or too low. Then, the while loop continues to run until the value of the guess is accurate enough and outputs it when done.
def binary_search_sqrt(number, tol=1e-6):
low, high = 0, number
guess = (low + high) / 2
while abs(guess * guess - number) > tol:
if guess * guess > number:
high = guess
else:
low = guess
guess = (low + high) / 2
return guess
number = 25
sqrt_estimate = binary_search_sqrt(number)
print(f"The square root of {number} is approximately {sqrt_estimate}")
Comparison of Approaches for Finding Square Root
Check out the given table for comparing the above-discussed approaches and their pros and cons:
| Approach | Description | Pros | Cons |
| Built-in Functions | Utilizes math.sqrt() or numpy.sqrt(). | Simple to use, suitable for basic calculations. | Limited customization and control. |
| Newton-Raphson Method | Iterative refinement based on tangent line approximation. | Rapid convergence, precise results. | Complexity in understanding and tuning. |
| Babylonian Method | Iterative approximation based on geometric mean. | Historical significance, relatively fast convergence. | May require more iterations for accuracy. |
| Binary Search Approach | Iterative narrowing of the search range. | Fast convergence, adaptable to varying precision requirements. | Requires a good initial range. |
That’s all from this informative guide related to finding the square root in Python.
Conclusion
While performing day-to-day tasks, finding square roots is not only a mathematical necessity but is also considered a practical programming skill. Therefore, in today’s guide, we discussed different approaches that can help you in tackling the square root problems easily.
From the simplicity of built-in functions to the elegance of the Newton-Raphson method, and the precision of binary search, we got you covered. Learn these approaches and calculate the square root efficiently in your Python program!
Want to explore and learn more related to Python, do check out our dedicated Python Tutorial Series!
